Artigo publicado na revista Crane Brasil nº 99. Acesse aqui!
As lingas, sejam elas de cabo de aço, cinta têxtil, corrente ou outro material, são elementos fundamentais para as operações de içamento, servindo como ligação entre a carga e o equipamento de guindar ou servindo como ligação com outras lingas ou acessórios.
A geometria, quase ilimitada, das cargas a serem içadas, traz desafios aos profissionais que escolhem, dimensionam e detalham as lingas. Portanto, ter ferramentas de cálculo eficazes que facilitem essas ações vai trazer segurança e eficácia operacional para os planos de movimentação de carga (planos de rigging).
Para o dimensionamento ou verificação das lingas, há alguns métodos consagrados, como o tabular, trigonométrico, do fator de uso, análise estrutural e outros, cada um com sua facilidade de implantação e resultados variando de otimizado a muito conservador.
A tabela seguinte resume três dos principais métodos, utilizados pelas normas brasileiras.
| VANTAGEM | DESVANTAGEM | ||
|---|---|---|---|
| Método tabular | Utiliza tabelas com os valores da Carga Máxima de Trabalho (CMT) (ou CMTE), para configurações de lingas mais usuais, variando a forma de amarração e o ângulo das pernas, adotando, geralmente 45° e 60° com a vertical. | Não necessita cálculo para determinação da CMT (ou CMTE), bastando a simples consulta em função da geometria e do parâmetro de referência da linga, que pode ser a CMT para vertical, no caso da cinta têxtil ou diâmetro no caso de cabo de aço ou corrente. | Limitação das variações de configurações e ângulos entre pernas Necessita de uma tabela para cada variação dos parâmetros, para lingas de cabo de aço (tipo de alma, categoria de resistência etc.). Probabilidade alta de, na tabela, haver valores errados por falha de digitação ou editoração. Pode levar ao superdimensionamento em valores limítrofes, como ângulo de 46° com a vertical, onde deve-se considerar, na tabela, coluna de 60°, reduzindo bastante a CMT (ou CMTE). |
| Método trigonométrico | Nas lingas de cabo de aço, são utilizadas fórmulas que consideram a carga de ruptura do cabo, eficiência do terminal e geometria da linga para determinação da CMT. | Não há necessidade de consulta às tabelas, sendo todos os parâmetros necessários obtidos em função do diâmetro do cabo, classe de resistência e tipo de terminal. Ideal para aplicação em planilhas eletrônicas ou programas de computador. Pode-se determinar a CMT para qualquer configuração de linga de 1 a 4 pernas. | Maior tempo para implementação. Difícil implementação para cintas têxteis e correntes. |
| Método do fato de uso (FU) | Utiliza fórmula matemática simples com parâmetros tabelados de CTM (ou CMTE) da linga para içamento vertical. | Determinação rápida da CMT (ou CMTE). Determinação imediata da força na perna da linga e nos acessórios conectados às pernas. | No caso das lingas de cabo de aço e corrente, dependem de se conhecer o valor da CMT para içamento vertical. Necessidade de consulta aos fatores de uso para linga em forca, linga assimétrica e cálculo adicional se houver dobramento da linga de cabo de aço no corpo. |
Como mostrado na tabela de métodos, o método do Fator de Uso reúne as vantagens do método tabular e do método trigonométrico, quando dispomos do valor da CMT para içamento vertical, que pode ser obtido de tabelas simplificadas, etiqueta ou plaqueta de identificação da linga.
O método do Fator de Uso tem como parâmetros o ângulo de inclinação das pernas da linga, a quantidade de pernas e a CMT da linga para a configuração de içamento vertical. Portanto, temos:
FU = N x Sen θ (Eq. 1)
CMTE = CMT x FU ou (Eq. 2)
CMTE = CMT x N x Sen θ (Eq. 3)
Sendo:
FU: Fator de uso.
CMTE: Carga máxima de trabalho efetiva da linga para a configuração proposta.
CMT: Carga máxima de trabalho da linga de 1 pernas para içamento vertical. Pode ser obtida da tabela de normas técnicas ou do catálogo do fabricante.
N: Número de pernas da linga, sendo 1 para linga de 1 pernas, 2 para linga de 2 pernas, 3 para linga de 3 ou 4 pernas.
θ: Ângulo da perna da linga com a horizontal.
Notas:
- o ângulo θ é referido em relação à horizontal e não em relação à vertical. As normas técnicas adotam frequentemente a referência vertical.
- A NBR 15637 a distinção entre CMT e CMTE. A CMT é a carga máxima de trabalho para linga de uma perna no içamento vertical, cujo valor é a referência para todos os demais cálculos. A CMTE é a carga máxima de trabalho para outras configurações aplicando o fator de uso sobre a CMT: forca, duas, três, quatro pernas, 2 pernas com forca etc.
- A NBR 13541-1 e NBR 15516-1, que tratam, respectivamente de lingas de cabo de aço e lingas de corrente, não distinguem CMT de CMTE, adotado simplesmente CMT.
- As normas brasileiras de lingas calculam suas tabelas com base no Fator de Uso.
Exemplos de aplicação
Exemplo 1: Qual a CMT de uma linga simétrica de cabo de aço com alma de fibra, diâmetro 19 mm, categoria de resistência 1770, com 2 pernas em ângulo com a horizontal de 60° (θ = 60°)?
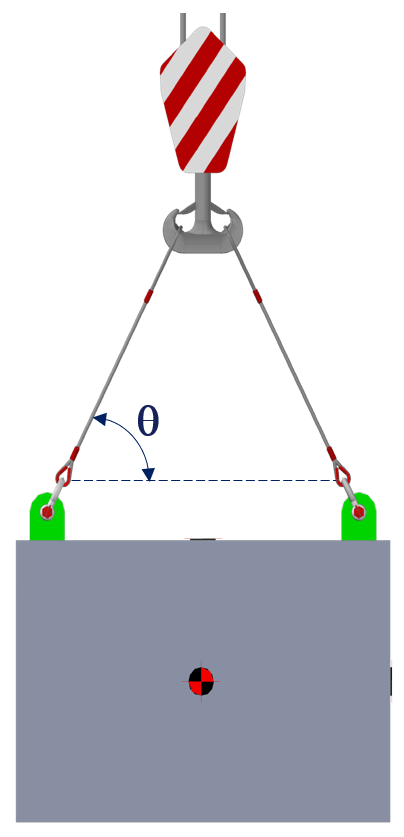
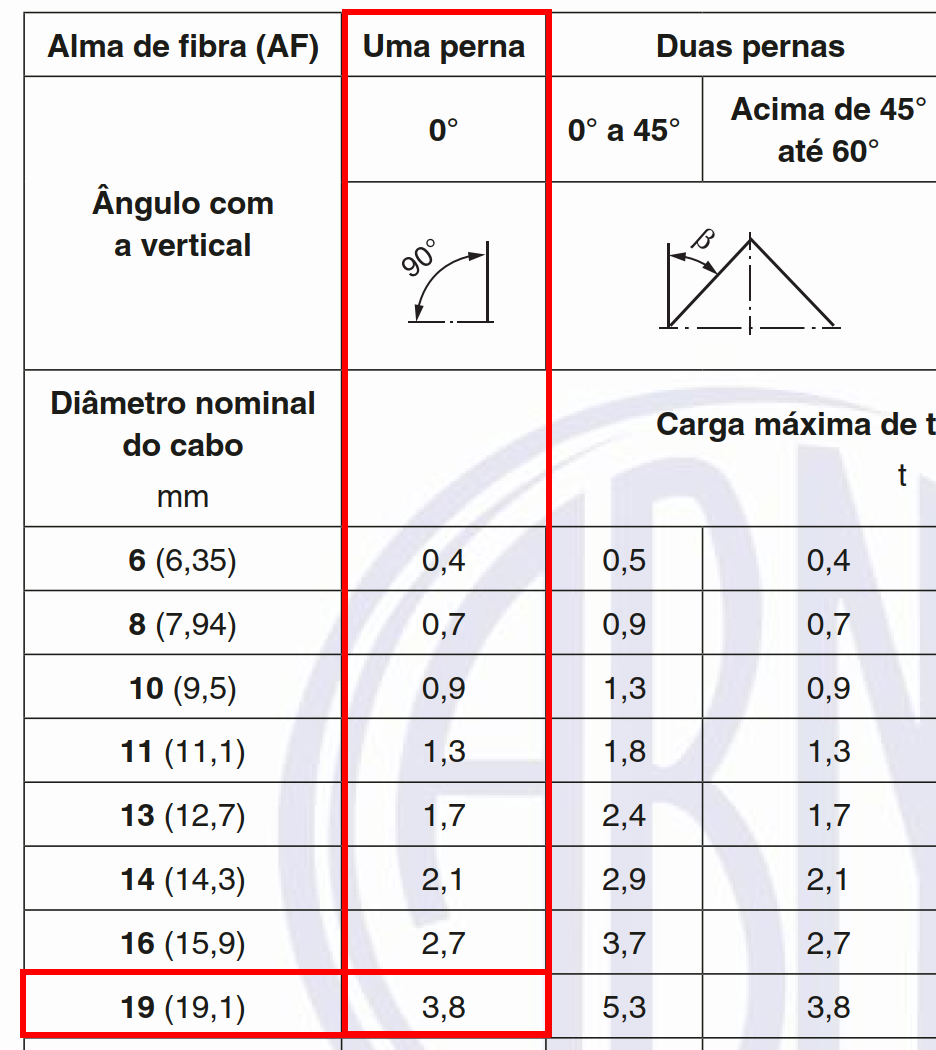
Baseado no extrato da Tabela 3 da NBR 13541-1 (2017), primeiramente, vamos determinar como se obter o valor da CMT para 2 pernas com ângulo de 45°, cujo valor tabelado é de 5,3 t.
FU45°,2p = N x Sen θ = 2 * Sen 45° = 1,4
CMT45°,19mm = CMTVert,19mm x FU45°,2p = 3,8 x 1,4 = 5,3 t
Agora, calculamos a CMT para o ângulo de 60° com a horizontal:
FU60°,2p = N x Sen θ = 2 * Sen 60° = 1,73
CMT60°,19mm = CMTVert,19mm x FU60°,2p = 3,8 x 1,73 = 6,5 t
Portanto, se fossemos usar o método tabular, a CMT para 60° com a horizontal seria 5,3 t, pois, a tabela da norma não apresenta o valor para este ângulo. Utilizando o FU específico para 60° com a horizontal, otimizamos o valor da CMT para 6,5 t. Um ganho de 22%.
O valor da CMT de 6,5 t significa que podemos içar com a linga de 2 pernas com ângulo de 60° com a horizontal, uma massa que induza na linga uma força máxima de 6,5 tf, devendo fazer parte dessa força os efeitos dinâmicos e variações possíveis de peso.
Para dimensionar a manilha que conecta uma das pernas à carga, basta escolhê-la conforme a CMT da linga de 1 perna.
CMTmanilha ≥ CMTVert,19mm ≥ 3,8 t
Portanto, podemos escolher uma manilha com CTM de 4,75 t, pois a força máxima em uma perna não ultrapassará 3,8 tf.
Agora que temos o FU para ângulo de 60° com a vertical (FU = 1,73), podemos calcular qualquer CMT para os outros diâmetros:
CMT60°,16mm = CMTVert,16mm x FU60°,2p = 2,7 x 1,73 = 4,6 t
CMT60°,14mm = CMTVert,14mm x FU60°,2p = 2,1 x 1,73 = 3,6 t
CMT60°,13mm = CMTVert,13mm x FU60°,2p = 1,7 x 1,73 = 2,9 t
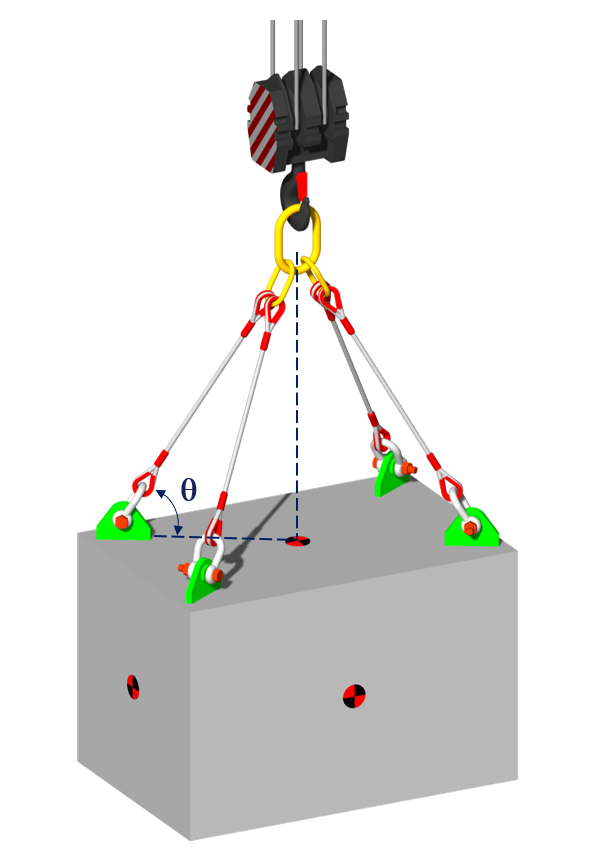
Exemplo 2: Agora, caso tenhamos uma linga de 4 pernas com as mesmas características, com θ = 60°, basta alterar o valor de N para 3.
FU60°,4p = N x Sen θ = 3 x Sen 60° = 2,59
CMT60°,19mm = CMTVert,19mm x FU60°,4p = 3,8 x 2,59 = 9,8 t
A manilha para esta configuração é a mesma da linga com 2 pernas, pois a força máxima continua sendo 3,8 tf em cada perna.
Para lingas de cintas têxteis, o procedimento é exatamente o mesmo.
Exemplo 3: Supondo o caso da Figura 4, utilizando cintas com CMT de 80 t (vertical), qual seria a CMTE da linga de 2 pernas em cada lado do balancim, para um ângulo de 60°?

Uma das vantagens das cintas é que não precisamos consultar a tabela para saber qual a CMT (vertical), bastando escolher aquela que desejamos utilizar.
Note que o Fator de Uso independe do tipo de material da linga, servindo para cabo de aço, cinta têxtil, corrente ou outro material.
Vamos calcular o CMTE dessa linga de 2 pernas para 45° e 60° com a horizontal.
CMTE45°,80t = CMTVert,80t x FU45°,2p = 80 x 1,4 = 112 t
CMTE60°,80t = CMTVert,80t x FU60°,2p = 80 x 1,73 = 138 t
CMTmanilha ≥ CMTVert,80t ≥ 80 t
Note que, para ambos os casos, a manilha permanece a mesma, pois a força máxima na perna é limitada ao valor da CMTVert,80t, isto é, nunca vamos utilizar uma perna mais carregada do que o limite da linga de 1 perna.
Se as 4 cintas fossem conectadas diretamente a um único gancho, teríamos a configuração de 4 pernas. Como no Exemplo 2 já calculamos o FU para 60° e 4 pernas, resta calcular a CMTE:
CMTE60°,80t = CMTVert,80t x FU60°,4p = 80 x 2,59 = 207 t
Caso desejemos utilizar essas lingas com ângulo de 45°, calculamos o novo Fator de Uso, a CMTE e a força na manilha:
FU45°,4p = N x Sen θ = 3 x Sen 45° = 2,12
CMTE45°,80t = CMTVert,80t x FU45°,4p = 80 x 2,12 = 169 t
CMTmanilha ≥ CMTVert,80t ≥ 80 t
Através dos exemplos, mostrou-se a facilidade do cálculo da CMT de lingas pelo método do Fator de Uso, que pode ser aplicado tanto no dimensionamento como na verificação de lingas de diversos materiais.
Como última recomendação, no cálculo da CMTE, a preferência é consultar os valores de CMTVert nas tabelas das normas técnicas.
O artigo completo pode ser lido na revista Crane Brasil nº 99.

GEOMETRIA E CARGA MÁXIMA DE TRABALHO EFETIVA DE LINGAS ASSIMÉTRICAS
As lingas de 2 pernas são muito utilizadas em içamentos diversos, sendo as simétricas facílimas de calcular. Porém, quando o centro de gravidade (CG) está deslocado do centro dos pontos de içamento, deve-se utilizar linga assimétrica, cujo cálculo não é trivial.
Neste “Como Calcular” é apresentada a formulação para determinação da geometria e da Carga Máxima de Trabalho Efetiva (CMTE) de lingas assimétricas com pontos de içamento nivelados e pontos de içamento desnivelados.
Com base nessas informações, é possível determinar um arranjo que leve ao içamento da carga nivelada, bem como dimensionar as manilhas, anel de carga e pontos de içamento.
Iniciando pela geometria, temos as duas situações ilustradas na Figura 1. A formulação para os pontos de içamento nivelados é um caso particular dos pontos desnivelados, fazendo H1 = H2 = H, podendo o leitor optar somente por trabalhar com a formulação deste último.
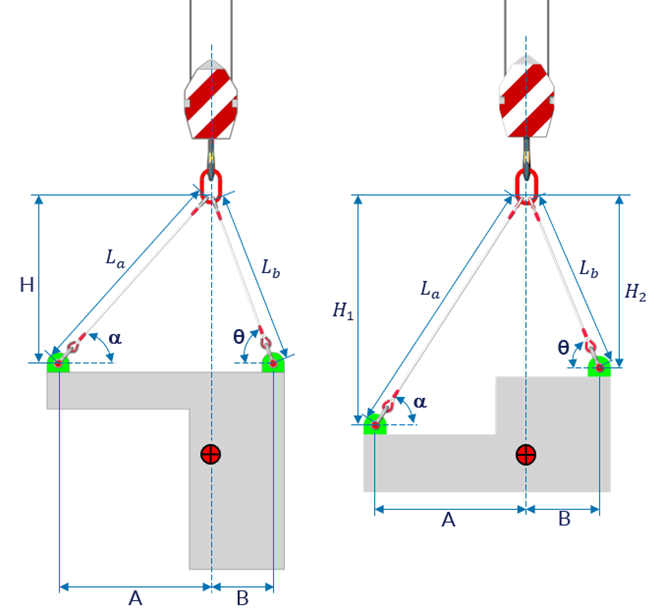
Onde:
A e B são as distâncias horizontais dos pontos de içamento ao centro de gravidade.
H, H1 e H2 são as distâncias verticais dos pontos de içamento até o ponto de interseção dos eixos das pernas.
La e Lb são os comprimentos das pernas somados com o comprimento das manilhas.
a e q são os ângulos das pernas com a horizontal.
Neste artigo, considera-se que o ângulo q é sempre maior que o ângulo a, garantindo que a perna “b”, que é a mais próxima do CG, será sempre a mais carregada.
Supondo que sejam conhecidas as dimensões A, B, H1 e H2, determinam-se os ângulos de inclinação com a horizontal:
α = tan-1
θ = tan-1
Com base nos ângulos ou nas demais dimensões, determinam-se os comprimentos das pernas e manilhas:
La = ou La =
Lb = ou Lb =
Para lingas com pontos de içamento nivelados, basta substituir, nas equações acima, H1 e H2 por H.
Uma vez determinada a geometria, utiliza-se o método do “fator de uso” para o cálculo da Carga Máxima de Trabalho Efetiva da linga em função da CMT vertical da linga utilizada na pena “b” (CMTb).

CMTE = CMTb
CMTE ≥ Fs
Onde:
CMTE é a Carga Máxima de Trabalho Efetiva da linga assimétrica.
CMTb é Carga Máxima de Trabalho referencial na sua forma vertical simples da perna “b”. Fs é a força total que a carga aplica na linga.
Nota 1:
A expressão trigonométrica de CMTE é o fator de uso (Fu), constante para uma determinada geometria, usado no cálculo imediato da CMTE para linga de qualquer material, seja de cabo de aço, cinta têxtil, corrente, cabo de HMPE e outros materiais, bastando multiplicar esse fator pela CMT da linga de uma perna na vertical.
Fu =
Nota 2:
A equação da CMTE acima, representa o caso geral da linga de 2 pernas, sendo a CMTEsim para a linga simétrica um caso particular em que a = q. Substituindo isso, temos:
CMTEsim = CMTb = CMTb 2sen(θ)
A expressão 2 sen(θ) é justamente o fator de uso da linga de 2 pernas simétrica.
Nota 3:
As normas técnicas de lingas não contemplam explicitamente o fator de uso de lingas assimétricas. Além disso, adotam como referência, o ângulo b, complementar ao ângulo com a horizontal:
β = 90º – θ
O leitor deve fazer as devidas conversões quando se referir aos ângulos das pernas.
Exemplo numérico
A linga assimétrica de 2 pernas, mostrada na Figura 3, será utilizada para içar uma carga que transmite 10,0 t à linga (Fs = 10,0 t, incluindo fatores dinâmicos, contingência, desvios de CG etc.). Calcular quais os cabos de aço e cintas têxteis devem ser utilizados para que a CMTE seja compatível com o carregamento. Calcular também as manilhas necessárias e o anel de carga.

Cálculo do fator de uso
Fu = = = 1,37
Com o valor de Fu, busca-se na norma do tipo de linga adotada, qual a CMTb que satisfaz a CMTE, ou pode-se determinar qual a CMT mínima necessária.
CMTE = CMTb Fu ≥ Fs
CMTb ≥ ≥ ≥ 7,3t
Portanto, a linga escolhida deve ter CMT mínimo de 7,3 t.
Utilizando uma linga de cabo de aço com alma de aço de cabo independente (AACI), categoria de resistência 1960, classe de construção 6×19 ou 6×36, recorre-se à Tabela 5 da NBR 13541-1, e na coluna “uma perna” selecionamentos um diâmetro que corresponda a um valor de CMT maior o igual a7,3 t. Neste caso, corresponde ao cabo com diâmetro de 26 mm, com CMT de 8,1 t.
Assim, a CMTE da linga assimétrica com cabo de aço (WR) pode ser calculada:
CMTEWR = CMTb Fu = 8,1 * 1,37 = 11,0t > 10,0t
Portanto, o cabo com diâmetro 26 mm atende. Testando o diâmetro de cabo imediatamente inferior (22 mm, CMT 6,1 t), vê-se que não atende ao carregamento:
CMTEWR = CMTb Fu = 6,1 * 1,37 = 8,3 < 10,0t
Para cálculo da CMTE da linga de cinta têxtil plana (CT), consulta-se a NBR 15637-1 e escolhe-se uma cinta com CMT maior ou igual a 7,3 t, que no caso é a cinta azul com CMT de 8 t. Calcula-se então a CMTE:
CMTECT = CMTb Fu = 8,0 * 1,37 = 10,9T > 10,0t
Para as manilhas, basta adotar aquelas com CMT maior ou igual a CMT da perna mais carregada. Neste exemplo, tanto para a linga de cabo de aço como para a cinta têxtil, a manilha mínima seria uma com CMT 8,5 t. Notar que, para a definição final das manilhas, deve-se verificar também a compatibilidade geométrica com o olhal da linga e com o olhal da carga.
Caso a linga possua anel de carga, este deve ter CMT maior ou igual a CMTE, que neste caso é 11 t.
Considerações Finais
O método do fator de uso permite o cálculo, de maneira simples, da CMTE de lingas com de materiais diversos a partir da CMT de referência de uma perna na vertical.
Nesta formulação, considerou-se que o ângulo da perna com a horizontal, do lado mais próximo ao CG, é sempre maior que o ângulo da outra perna. Isso garante que a perna mais próxima será sempre a mais carregada.
As duas pernas da linga, apesar de terem comprimentos diferentes, devem ser idênticas na composição, sendo governadas pela de maior solicitação. Isso vale também para os acessórios nos pontos de içamento.
O artigo completo pode ser lido na revista Crane Brasil nº 102.







